W jednym z poprzednich wpisów (Wartość bieżąca pieniądza – dyskontowanie proste) poruszyłem tematykę dyskontowania. Dokładniej rzecz biorąc, wpis dotyczył dyskontowania prostego, czyli takiego, które nie uwzględnia kapitalizacji w czasie. W rzeczywistości zdecydowanie częściej spotykamy się z dyskontowaniem składanym. Dotyczy to w szczególności okresów powyżej jednego roku. Warto zatem wiedzieć jak podchodzić do tego typu zadań.
Pojęcie dyskontowania składanego pomogą nam zrozumieć przykłady przedstawione poniżej. Rozwiązywać je będziemy oczywiście przy wykorzystaniu stosownego wzoru (poniżej). Warto wiedzieć, że jest to przekształcony wzór na przyszłą wartość pieniądza – dokładnie opisany we wpisie Wartość przyszła pieniądza – oprocentowanie złożone.
Przykład 1:
Nowak jest winny Kowalskiemu 900 zł. Obiecał mu oddać środki jutro, niemniej zaproponował, że jeśli Kowalski przedłuży termin zwrotu o dwa lata, to odda mu 1 050 zł. Czy Kowalski powinien się zgodzić na propozycję? Oprocentowanie lokaty dwuletniej z kapitalizacją roczną w jego banku wynosi 6%.
Do rozwiązania powyższego zadania przydatny będzie poniższy wzór:
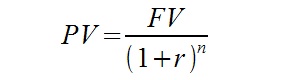
Oznaczenia:
FV – wartość przyszła (Future Value)
PV – wartość bieżąca (Present Value)
n – ilość okresów
r – oprocentowanie
Przejdźmy zatem do rozwiązania przykładu. Wartość bieżąca pożyczki to 900 zł.Jest to wartość dla wariantu pierwszego. Wariantem drugim będzie propozycja Nowaka – z tym, że tu mamy daną jedynie wartość przyszłą. Wykorzystajmy zatem powyższy wzór by obliczyć jej wartość bieżącą. Posiadamy wszystkie niezbędne dane.
PV = 1 050 / (1 + 0,06)^2
PV = 1 050 / 1,1236
PV = 934,50 zł
Wartość bieżąca sumy zaproponowanej przez Nowaka w wariancie drugim jest większa od wartości bieżącej dla wariantu pierwszego. Stąd też Kowalski powinien zgodzić się na przedstawioną propozycję wydłużenia terminu spłaty pożyczki.
Przykład 2:
Nowak jest winny Kowalskiemu 1 800 zł. Obiecał mu oddać środki jutro, niemniej zaproponował, że jeśli Kowalski przedłuży termin zwrotu o półtora roku, to odda mu 2 000 zł. Czy Kowalski powinien się zgodzić na propozycję? Oprocentowanie lokaty półtorarocznej z kapitalizacją półroczną w jego banku wynosi 5%.
Na potrzeby rozwiązania tego przykładu uzupełnimy pierwszy wzór o możliwość zastosowania kapitalizacji śródrocznej:
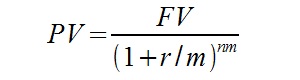
Oznaczenia:
FV – wartość przyszła (Future Value)
PV – wartość bieżąca (Present Value)
n – ilość okresów
m – ilość kapitalizacji w jednym okresie (np. w ciągu roku)
r – oprocentowanie
Mając wzór przystępujemy do rozwiązania zadania. Dyskontujemy propozycję Nowaka.
PV = 2 000 / (1 + 0,05/2)^1,5*2
PV = 2 000 / 1,0769
PV = 1 857,20 zł
Wartość bieżąca pożyczki w nowym wariancie zaproponowanym przez Nowaka jest wyższa od kwoty jaką miałby zwrócić w dniu jutrzejszym. Kowalski zatem powinien przystąpić na propozycję.
Witam,
wydaje mi się że w przykładzie 1 odpowiedź jest błędna ( tzn. Kowalski powinien zgodzić się na propozycję Nowaka bo wartość bieżąca w 2 wariancie – z przedłużeniem terminu spłaty jest wyższa od wariantu 1)
Czy mam rację??
Proszę o sprawdzenie.
Tak, ma Pani rację. Wpis poprawiłem (obliczenia właściwe, błąd jedynie w tekście odpowiedzi). Przepraszam wszystkich czytelników za niedopatrzenie.
Witam,
czy w przykładzie 2 m powinno = 3, ponieważ kapitalizacja jest co pół roku w 1,5 rocznym okresie lokaty?
wówczas :
PV = 2000/(1+0,05/3)^1,5*3
PV = 2000 / 1,077
PV = 1856,63
„m” to ilość kapitalizacji w jednym okresie, w tym przypadku 2. Obliczenia są zatem prawidłowe. Proszę jednak zwrócić uwagę na to, że mamy 1,5 okresu (półtora roku). Stąd 2 * 1,5 = 3. Pan niepotrzebnie pomnożył ponownie przez 1,5.