Matematyka Finansowa.pl

Załóżmy, że kilka lat temu założyliśmy lokatę bankową. Jej oprocentowanie było zmienne. Po upływie okresu deponowania otrzymaliśmy odsetki wraz z włożonym kapitałem. Tylko ile tak na prawdę zarobiliśmy? W odpowiedzi na to pytanie pomaga pojęcie efektywnej stopy procentowej. Jest to taka stopa, która bierze pod uwagę sposób naliczania odsetek (kapitalizacji). Co ważne, efektywna stopa procentowa jest najczęściej wykorzystywana wtedy, gdy zakładana jest roczna kapitalizacja. Jeśli porównujemy zyski z dwóch inwestycji o różnych okresach kapitalizacji, efektywna stopa procentowa sprawdzi się idealnie. Pokaże ona bowiem realne zyski odnosząc się do kapitalizacji co 12 miesięcy. Jednocześnie efektywną stopę procentową możemy także wykorzystać w zadaniach porównujących inwestycje o różnych okresach zapadalności.

Poniżej przedstawiam wzór oraz kilka przykładów, które pomogą nam zrozumieć pojęcie efektywnej stopy procentowej. Tematyka jest prosta, tym bardziej zachęcam do jej opanowania.

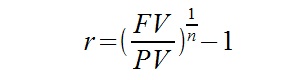
FV – wartość przyszła (Future Value)
PV – wartość bieżąca (Present Value)
n – ilość okresów (lat)
r – efektywna stopa procentowa

Przykład 1:
Kowalski wpłacił 5 000 zł 3 lata temu na konto oszczędnościowe w banku. Dziś stan konta wynosi otrzymał 5 650 zł. Jakie było efektywne oprocentowanie rachunku na przestrzeni 3 lat?

Zadanie jest bardzo proste, wystarczy że podstawimy podane w treści dane do powyższego wzoru.

r = (5 650/5 000)^(1/3) – 1
r = 1,13^(1/3) – 1
r = 0,0416
r = 4,16%

Efektywne oprocentowanie rachunku oszczędnościowego wyniosło 4,16%.

Przykład 2:
Doradca zaproponował Kowalskiemu 24-miesięczną lokatę bankową. Od każdej wpłaty w wysokości 2 000 zł bank po 2 latach naliczy 10% odsetek. Jakie jest efektywne oprocentowanie lokaty?

W powyższym zadaniu mamy daną wartość bieżącą, ale nie znamy wartości przyszłej. Należy ją zatem obliczyć.

FV = 2 000 * (1 + 0,10)
FV = 2 000 * 1,10
FV = 2 200 zł

Mając FV i PV możemy obliczyć efektywne oprocentowanie lokaty bankowej.

r = (2 200/2 000)^(1/2) – 1
r = 1,10^(1/2) – 1
r = 0,0488
r = 4,88%

Efektywne oprocentowanie lokaty w banku wyniesie 4,88%. Jest ono mniejsze od oprocentowania nominalnego, ponieważ zakłada częstszą kapitalizację.

Przykład 3:
Kowalski 10 lat temu na rachunek rozliczeniowo oszczędnościowy w swoim banku wpłacił 8 000. Niestety zapomniał o tych pieniądzach. Dziś, przy okazji wizyty w oddziale banku, otrzymał informację, że posiada na koncie 8 500 zł. Doradca zaproponował zakup z tych środków jednostek uczestnictwa funduszy inwestycyjnych. Kowalski chciałby jednak wiedzieć jakie było efektywne oprocentowanie jego środków zgromadzonych na ROR.

Wszystkie dane niezbędne do podstawienia do wzoru zaprezentowanego w niniejszym wpisie mamy dane. Obliczamy zatem efektywne oprocentowanie ROR.

r = (8 500/8 000)^(1/10) – 1
r = 1,0625^(1/10) – 1
r = 0,0061
r = 0,61%

Efektywne oprocentowanie rachunku oszczędnościowo-rozliczeniowego Kowalskiego na przestrzeni 10 lat wyniosło 0,61%. Mało. Niestety rachunki ROR nie służą do oszczędzania, Kowalski popełnił błąd nie interesując się swoimi oszczędnościami.