Płatności systematyczne – oprocentowanie złożone (cz. 1)

Wysłane przez admin dnia 19 lutego 2011 Zostaw komentarz3 komentarze Idź do komentarzy

W jednym z poprzednich wpisów (Płatności systematyczne – oprocentowanie proste) omówiłem tematykę płatności systematycznych przy oprocentowaniu prostym. W rzeczywistości spotykamy się zazwyczaj z oprocentowaniem złożonym. Stąd poprzednie rozważania można uznać za typowo teoretyczne. Przeanalizujmy zatem prosty przykład.

Przykład 1:
Klient zamierza przez 10 lat wpłacać po 1 000 zł rocznie na konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego roku, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie (kapitalizacja roczna). Ile odsetek (łącznie) klient otrzyma po 3, 7 i 10 latach oszczędzania?

W tym przykładzie mamy do czynienia z problemem systematycznego oszczędzania przy kapitalizacji złożonej (odsetki są dopisywane raz w roku i powiększają uzbierany kapitał). Poniższy wzór pomoże nam w rozwiązaniu zadania:

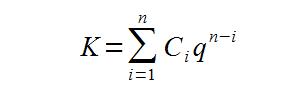
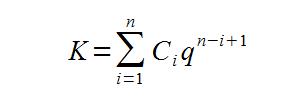
q = 1 + r

Oznaczenia:
K – łączna kwota wpłat powiększonych o naliczone odsetki
C_i – przepływ pieniężny, kwota i-tej wpłaty
n – łączna ilość wpłat
r – oprocentowanie

Pierwszy wzór stosuje się przy płatnościach systematycznych z dołu, tzn. na końcu roku. Drugi natomiast dotyczy płatności systematycznych z góry – na początku roku (inaczej: z wyprzedzeniem).

Podstawmy zatem dane z przykładu do powyższego wzoru (drugiego):
K3 = 1 000 * (1 + 0,06)^(3 – 1 + 1) + 1 000 * (1 + 0,06)^(3 – 2 + 1) + 1 000 * (1 + 0,06)^(3 – 3 + 1)
K3 = 1 000 * 1,19 + 1 000 * 1,12 + 1 000 * 1,06
K3 = 3 374,62 zł

Po 3 latach oszczędzania Klient otrzyma 374,62 zł odsetek. A ile po 7 i 10 latach?

K7 = 1 000 * (1 + 0,06)^(7 – 1 + 1) + 1 000 * (1 + 0,06)^(7 – 2 + 1) + 1 000 * (1 + 0,06)^(7 – 3 + 1) + 1 000 * (1 + 0,06)^(7 – 4 + 1) + 1 000 * (1 + 0,06)^(7 – 5 + 1) + 1 000 * (1 + 0,06)^(7 – 6 + 1) + 1 000 * (1 + 0,06)^(7 – 7 + 1)
K7 = 8 897,47 zł

K10 = 1 000 * (1 + 0,06)^(10 – 1 + 1) + 1 000 * (1 + 0,06)^(10 – 2 + 1) + 1 000 * (1 + 0,06)^(10 – 3 + 1) + 1 000 * (1 + 0,06)^(10 – 4 + 1) + 1 000 * (1 + 0,06)^(10 – 5 + 1) + 1 000 * (1 + 0,06)^(10 – 6 + 1) + 1 000 * (1 + 0,06)^(10 – 7 + 1) + 1 000 * (1 + 0,06)^(10 – 8 + 1) + 1 000 * (1 + 0,06)^(10 – 9 + 1) + 1 000 * (1 + 0,06)^(10 – 10 + 1)
K10 = 13 971,64 zł

Po 7 latach Klient otrzyma 1 897,47 zł odsetek, natomiast po 10 latach 3 971,64 zł.