Załóżmy, że co jakiś czas wpłacamy stałą kwotę pieniędzy. Pieniądze te są oprocentowane, ale instytucja finansowa nie oferuje kapitalizacji odsetek – są one wypłacane po każdym okresie rozliczeniowym. Klient zatem gromadzi na koncie jedynie swój kapitał. Jak policzyć ile łącznie odsetek zostanie wypłaconych po X latach?
Nie jest to trudne. Skorzystać można z wzoru podanego poniżej. Warto jednak podkreślić, że ma on (podobnie jak przykład) zastosowanie głównie teoretyczne. W praktyce jest tak, że banki kapitalizują odsetki (chociażby raz w roku). Na tym w dużej mierze polega magia systematycznego oszczędzania – odsetki pracują na kolejne odsetki co oznacza, że zakładany poziom uzbieranego kapitału uda się znacznie szybciej osiągnąć.
Ale po kolei. Teraz zajmę się oprocentowaniem prostym, natomiast w innym wpisie przedstawię złożone. Zacznijmy jednak od danych do przykładu.
Przykład 1:
Klient zamierza przez 10 lat wpłacać po 1 000 zł rocznie na specjalnie utworzone konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego roku, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie, odsetki wypłaca jednak na koniec okresu oszczędzania. Ile odsetek (łącznie) klient otrzyma po 3, 7 i 10 latach oszczędzania?
Najpierw zapoznamy się z obiecanym wzorem:
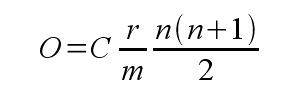
Oznaczenia:
O – łączna kwota odsetek
C – przepływ pieniężny, kwota wpłaty
r – oprocentowanie
m – ilość regularnych wpłat w ciągu roku
n – łączna ilość wpłat
Podstawmy zatem dane z przykładu do powyższego wzoru:
O3 = 1 000 zł * 0,06/1 * (3 * 4)/2 = 360 zł
Po 3 latach klient otrzyma łącznie 360 zł odsetek. Teraz krótkie uzasadnienie:
Klient trzymał 180 zł odsetek z 1 000 zł wpłaconych na samym początku inwestycji (po 6%, czyli 60 zł na koniec każdego roku). Otrzymał także 120 zł z 1 000 zł wpłaconych na początku drugiego roku oszczędzania (60 zł na koniec drugiego roku oraz 60 zł na koniec drugiego roku). Ostatecznie otrzymał także 60 zł odsetek za 1 000 zł, które wpłacił na początku trzeciego roku inwestycji. Te środki trzymał tylko 12 miesięcy, zatem otrzymał 60 zł odsetek. Podsumowując: 180 zł + 120 zł + 60 zł = 360 zł.
Obliczmy jeszcze łączną kwotę odsetek po 7 i 10 latach oszczędzania:
O7 = 1 000 zł * 0,06/1 * (8 * 7)/2 = 1 680 zł
O10 = 1 000 zł * 0,06/1 * (11 * 10)/2 = 3 300 zł
Widać zatem wyraźnie, że im dłużej klient oszczędza, tym większe odsetki dostaje. Dzieje się tak, ponieważ uzbierany po latach kapitał jest znacznie większy niż na początku oszczędzania.
w pierwszym przykladzie jest bład, wynik jest dobry ale n+1 jest rowne 2 a powinno wyjsc rowne 4
Poprawiłem, dziękuję za spostrzegawczość.
Jeżeli bank kapitalizuje odsetki co roku (a to jest jedyne logiczne wyjście w tej sytuacji), to klient otrzyma:
1191,02 z pierwszego tysiąca złotych (1000 zł * 1,06 * 1,06 * 1,06)
1123,60 z drugiego tysiąca
1060 z trzeciego tysiąca
czyli razem odsetek: 374,62 zł. Zgadza się?
ok, teraz zauważyłem, że „instytucja finansowa nie oferuje kapitalizacji odsetek”, zwracam honor:) swoją drogą szkoda, że blog leży od prawie 2 lat.
Bank powinien naliczać procenty od procentów . Po trzech latach kwota będzie większa niż podane 360 zł. Jeżeli tego nie robi to okrada klienta. Z pierwszego 1000zł po trzech latach powinno się doliczyć 191 zł ,a nie 180zł