Matematyka Finansowa.pl

W poprzednim wpisie (Przeciętna stopa procentowa – oprocentowanie proste (cz. 1)) omówiłem sposób liczenia przeciętnej stopy procentowej. Okazuje się jednak, że w codziennym życiu bardzo często spotykamy się z zadaniami, które wymagają głębszej analizy. Przeanalizujmy zatem typowe problemy.

Przykład 1:
Kowalski posiada dwa kredyty bankowe zaciągnięte na następujących warunkach:
– 5 000 zł na 7 miesięcy z oprocentowaniem 17% w skali roku,
– 1 800 zł na 3 miesiące z oprocentowaniem 15% w skali roku.
Kowalski chciałby zamienić oba kredyty na jeden. Jakie maksymalne oprocentowanie powinien zaakceptować by operacja okazała się opłacalna?

Jak rozwiązać takie zadanie? Z wzoru na przeciętną stopę procentową moglibyśmy skorzystać, gdyby nie jeden szczegół – różne kwoty zaciągniętych kredytów. Musimy zatem skorzystać z innego wzoru, uwzględniającego zróżnicowane warunki transakcji. Przedstawiam go poniżej:

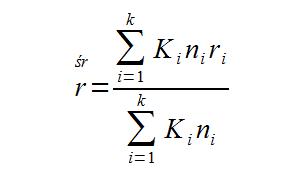
Oznaczenia:
r^śr – średnie oprocentowanie
n_i – długość podokresu z danym oprocentowaniem (r_i)
r_i – oprocentowanie w podokresie n_i
K_i – wysokość i-tej pożyczki/ lokaty…

Mając odpowiedni wzór możemy przystąpić do rozwiązania.
r^śr = (5 000 * 7/12 * 0,17 + 1 800 * 3/12 * 0,15) / (5 000 * 7/12 + 1 800 * 3/12)
r^śr = 563,33 / 3 366,67
r^śr = 0,1673
r^śr = 16,73%
Kowalski nie powinien akceptować oprocentowania nowego kredytu wyższego niż 16,73%.

Przykład 2:
Kowalski posiada cztery kredyty bankowe w Banku A, które chciałby skonsolidować. Ten sam Bank A zaproponował mu zmianę oprocentowania dla wszystkich kredytów, byłoby to 17%. Okresy kredytowania poszczególnych kredytów pozostałyby bez zmian. Określ czy jest to opłacalna operacja. Warunki poszczególnych pożyczek przedstawia poniższe zestawienie:
– 12 000 zł na 12 miesięcy z oprocentowaniem 14% w skali roku,
– 2 300 zł na 12 miesięcy z oprocentowaniem 18% w skali roku.
– 27 000 zł na 9 miesięcy z oprocentowaniem 19% w skali roku,
– 8 800 zł na 2 miesiące z oprocentowaniem 16% w skali roku.

Rozwiązanie:
Korzystamy z tego samego wzoru co w poprzednim przykładzie. Oto co otrzymujemy:
r^śr = (12 000 * 12/12 * 0,14 + 2 300 * 12/12 * 0,18 + 27 000 * 9/12 * 0,19 + 8 800 * 2/12 * 0,16) / (12 000 * 12/12 + 2 300 * 12/12 + 27 000 * 9/12 + 8 800 * 2/12)
r^śr = 6 176,17 / 36 016,67
r^śr = 0,1715
r^śr = 17,15%
Bank A zaproponował korzystne rozwiązanie dla Klienta (średnie oprocentowanie jego zobowiązań spadnie z 17,15% do 17%).