Matematyka Finansowa.pl

W poprzednim wpisie (Płatności systematyczne – oprocentowanie złożone (cz. 1)) przedstawiłem podstawowe informacje o płatnościach systematycznych przy oprocentowaniu złożonym. Warto rozwinąć ten temat, szczególnie że w niektórych przypadkach możemy znacząco uprościć sposób rozwiązywania zadań.

Zacznijmy od wykorzystania wzoru na sumę ciągu geometrycznego. Wzór ten możemy zastosować, gdy poszczególne wartości poszczególnych przepływów pieniężnych są równe. Dodatkowym warunkiem jest stałość oprocentowania w czasie.

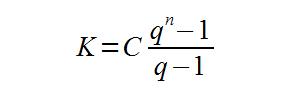
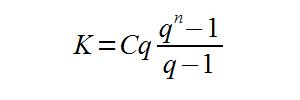
q = 1 + r
q ≠ 1

Oznaczenia:
K – łączna kwota wpłat powiększonych o naliczone odsetki
C – przepływ pieniężny
n – łączna ilość wpłat
r – oprocentowanie

Pierwszy wzór stosuje się przy płatnościach systematycznych z dołu, tzn. na końcu roku. Drugi natomiast dotyczy płatności systematycznych z góry – na początku roku (inaczej: z wyprzedzeniem).

Przykład 1:
Klient zamierza przez 10 lat wpłacać po 1 000 zł rocznie na konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego roku, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie (kapitalizacja roczna). Ile odsetek (łącznie) klient otrzyma po 3, 7 i 10 latach oszczędzania?

W zadaniu mamy do czynienia z płatnościami systematycznymi z góry. Stosujemy zatem drugi z wzór.

K3 = 1 000 * 1,06 * ((1,06^3 – 1)/(1,06 – 1))
K3 = 1 060 * 3,18
K3 = 3 374,62

K7 = 1 000 * 1,06 * ((1,06^7 – 1)/(1,06 – 1))
K7 = 1 060 * 8,39
K7 = 8 897,47

K10 = 1 000 * 1,06 * ((1,06^10 – 1)/(1,06 – 1))
K10 = 1 060 * 13,18
K10 = 13 971,64

Przykład 2:
Kowalski zamierza oszczędzać na emeryturę. Policzył, że będzie mógł rocznie odłożyć 800 zł. Wpłaty będzie dokonywał na specjalnie utworzony program systematycznego oszczędzania. Jaką kwotę uzbiera po 30 latach przy założeniu 6%, 7% oraz 8% stopy zwrotu.

Także w tym zadaniu mamy do czynienia z płatnościami systematycznymi z góry. Stosujemy zatem drugi z wzór.

Wyliczenie dla 6% rocznej stopy zwrotu:
K = 800 * 1,06 * ((1,06^30 – 1)/(1,06 – 1))
K = 848 * 79,06
K = 67 041,34

Wyliczenie dla 7% rocznej stopy zwrotu:
K = 800 * 1,07 * ((1,07^30 – 1)/(1,07 – 1))
K = 856 * 94,46
K = 80 858,43

Wyliczenie dla 8% rocznej stopy zwrotu:
K = 800 * 1,08 * ((1,08^30 – 1)/(1,08 – 1))
K = 864 * 113,28
K = 97 876,69

Analizując powyższe przykłady łatwo zauważyć, że im większa oczekiwana stopa zwrotu, tym większe zyski po x-latach oszczędzania. Warto jednak dodać, że ryzyko związane z inwestycją jest także wyższe.