Osoby zaciągające kredyt mają najczęściej do wyboru dwa rodzaje rat: równe i malejące. W tym wpisie przedstawię metodę wyliczania wysokości raty równej. Z moich obserwacji wynika, że zdecydowanie większa liczba Polaków wybiera ten sposób spłaty kredytu. Warto zatem pamiętać, że charakteryzuje się on większym całkowitym kosztem kredytu.
Generalnie do wyliczenia wysokości raty równej służy dość skomplikowany wzór. Oto on:
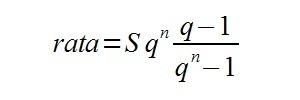
q = 1 + r/m
Oznaczenia:
S – kwota zaciągniętego kredytu (kwota brutto, wraz z kosztami okołokredytowymi)
n – ilość rat
r – oprocentowanie nominalne dla okresu
m – ilość rat w okresie (najczęściej w roku)
Przykład 1:
Kowalski postanowił zaciągnąć szybki kredyt gotówkowy z swoim banku. Potrzebuje 4 000 zł. Bank zaproponował oprocentowanie 17,90%. Jaką ratę równą zapłaci Kowalski zakładając 24-miesięczny okres kredytowania? Bank pobiera prowizję za przyznanie kredytu w wysokości 210,53 zł i jest ona kredytowana.
Podstawiamy zatem dane do wzoru:
rata = 4 210,53 * (1 + 0,179/12)^24 * ((1 + 0,179/12 – 1)/((1 + 0,179/12)^24 – 1))
rata = 210
Rata równa kredytu wyniesie 210 zł.
Sprawdźmy jeszcze ile wyniesie całkowity koszt kredytu.
W całym okresie kredytowania Kowalski wpłaci do banku 24 raty po 210 zł. Łącznie jest to 5 040 zł. Pożyczył od banku 4 000 zł netto. Stąd też całkowite koszty związane z kredytem wyniosą 1 040 zł.
Przykład 2:
Bank A posiada w ofercie promocję kredytu gotówkowego. 2 000 zł można otrzymać bez prowizji i innych kosztów okołokredytowych na okres 12 miesięcy. Oprocentowanie takiego kredytu to 19% w skali roku. Bank B zaś prowizję pobiera w wysokości 100 zł, ale oprocentowanie wynosi już jedynie 12% (kwota kredytu netto i okres kredytowania pozostają takie same). Która oferta jest korzystniejsza?
Aby w tym przykładzie sprawdzić, który bank ma korzystniejszą ofertę kredytu gotówkowego należy policzyć wysokość raty równej.
rataA = 2 000 * (1 + 0,19/12)^12 * ((1 + 0,19/12 – 1)/((1 + 0,19/12)^12 – 1))
rataA = 184,31
rataB = 2 100 * (1 + 0,12/12)^12 * ((1 + 0,12/12 – 1)/((1 + 0,12/12)^12 – 1))
rataB = 186,58
Mimo wyższego oprocentowania, korzystniejsza jest oferta Banku A (rata jest niższa o 2,27 zł). Bank ten nie pobiera prowizji za przyznanie kredytu.
Witam,
czy ten wzór jest aby napewno poprawny? nie jest on w ogóle uzależniony od dnia płatności. Zatem nie uwzględnia 1) ilości dni w miesiącu, ani 2) okresu od zawarcia umowy do spłaty pierwszej raty-który zwykle nie jest pełnym miesięcznym okresem. Wydaje mi się, że tak obliczona rata jest nie wiadomo jak dobrym przybliżeniem realnej raty. W związku z czym porównywanie kredytów i stwierdzenie, że któryś jest korzystniejszy na podstawie takich wyliczeń mija się z celem, bo te 2,27 może równie dobrze stanowić błąd.
Pozdrawiam
Kamil
Tak, wzór jest poprawny. Podstawiamy parametry dwóch banków do tego samego wzoru (zakłada płatność raty równo po miesiącu), więc korzystniejsza jest oferta z niższą ratą. Jeśli zaś chodzi o drugą sprawę, którą Pan poruszył – dzień płatności, to jest to trochę bardziej skomplikowane. Możliwe, że poruszę tę tematykę w przyszłości. Banki najczęściej stosują raty wyrównujące (pierwsza lub ostatnia).
Można wykorzystać funkcję PMT w Excelu
=PMT(oprocentowanie roczne/12;liczba rat;-1*kwota kredytu)
Coś jest nie tak z tym wzorem do Excela 🙁
Wszędzie powiela się wzór na ratę oparty o zasadę, że każdy miesiąc jest równy a niestety tak nie jest! Skoro banki mają ambicję liczenia z „dokładnością” do jednego dnia (powinno być doby)to może ktoś ujawni jakiego wzoru używa bank aby zapewnić tą dokładność. Powinien to być ten sam wzór, pochodzący z umorzeniowego równania bilansowego tyle, że składniki szeregu sumy powinny zawierać miesiące o rzeczywistej długości bez zabiegu wyrównania ich długości w celu zastosowania wzoru na sumę szeregu geometrycznego. Po co zwijać szereg co powoduje nieścisłość wyniku mogąc, w tym samym komputerze, obliczyć dokładny wynik z wyliczenia pełnej postaci szeregu ?
Wzór powinien być taki:
rata = S * suma_po_n( q^(-t_n * m ) gdzie t_n – kolejne miesiące kredytu. Reszta jak w sztandarowym wzorze na tej stronie. Może ktoś ma inny pomysł ???
W prosty sposób można wyliczyć kalkulatorem finansowym. To taki sposób dla niefinansistów.