Tym razem kontynuujemy cykl wpisów na temat płatności systematycznych. Poprzednie wpisy znajdują się pod adresami:
– Płatności systematyczne – oprocentowanie złożone (cz. 1)
– Płatności systematyczne – oprocentowanie złożone (cz. 2))
– Płatności systematyczne – oprocentowanie złożone (cz. 3))
Dotychczas przedstawiłem metody obliczania przyszłej wartości regularnych wpłat o okresach rocznych lub śródrocznych. Zastosowanie miały także wzory na ciągi geometryczne, które znacząco upraszczały obliczenia. We wszystkich przykładach stosowaliśmy zaś oprocentowanie złożone, dzięki czemu miały one rzeczywisty charakter. Niemniej zadania, które przedstawiałem miały jedno główne założenie – okresy kapitalizacji i kolejnych wpłat są równe. Tym razem zrezygnujemy z tego założenia. Niestety znacząco podniesie to poziom trudności rozwiązywanych zadań. Będziemy mieli do czynienia z dwoma wariantami zadań:
– kapitalizacja jest częstsza niż okresy wpłaty,
– okresy wpłaty są częstsze niż kapitalizacja.
By jak najlepiej zrozumieć sens zastosowania asymetrycznych okresów kapitalizacji i okresów kolejnych wpłat, zaczniemy od przykładu.
Przykład 1:
Klient zamierza przez 10 lat wpłacać po 1 000 zł kwartalnie na konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego kwartału, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie (kapitalizacja roczna). Ile odsetek (łącznie) klient otrzyma po 10 latach oszczędzania?
Jaką sytuację mamy w zadaniu? Otóż okresy wpłaty są częstsze niż kapitalizacja. Klient będzie wpłacał środki raz na kwartał a bank będzie naliczał oprocentowanie raz w roku. Tzn. że pierwsza wpłata będzie „pracowała” na odsetki przez 12 miesięcy, druga przez 9, trzecia przez 6 miesięcy itp. Z takim przypadkiem nie mieliśmy jeszcze do czynienia. Możemy oczywiście policzyć wszystko ręcznie, ale ma to sens jedynie przy krótkich okresach inwestycji. Dla dłuższych polecam stosowanie poniższych wzorów.
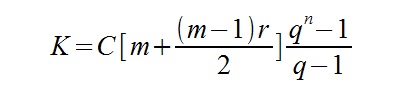
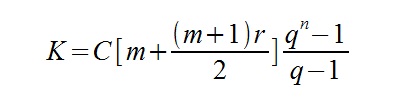
q = 1 + r
Oznaczenia:
K – łączna kwota wpłat powiększonych o naliczone odsetki
C – przepływ pieniężny
n – ilość okresów (lat)
m – ilość wpłat w jednym okresie (np. roku)
r – oprocentowanie w danym okresie (roku)
Pierwszy wzór ma zastosowanie przy płatnościach systematycznych z dołu, tzn. na końcu okresu kapitalizacji (miesiąca/ kwartału/ roku/ …). Drugi natomiast stosuje się przy płatnościach systematycznych z góry – na początku okresu kapitalizacji (inaczej: z wyprzedzeniem).
W zadaniu mamy do czynienia z płatnościami systematycznymi z góry. Stosujemy zatem drugi z wzór.
K10 = 1 000 * (4 + ((4 + 1) * 0,06) / 2) * (((1,06)^10 – 1)/(1,06 – 1))
K10 = 54 700,30 zł
Po 10 latach Klient uzbiera łącznie ponad 54 700 zł. Ile jednak z tej kwoty stanowią uzyskane odsetki?
O = 54 700,30 – 10 * 4 * 1 000
O = 54 700,30 – 40 000
O = 14 700,30 zł
Klient zarobi w ciągu 10 lat 14 700,30 zł.
Przykład 2:
Klient zamierza przez 10 lat wpłacać po 1 000 zł rocznie na konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego roku, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie (kapitalizacja półroczna). Ile odsetek (łącznie) klient otrzyma po 10 latach oszczędzania?
Jaką sytuację mamy w zadaniu? Otóż okresy wpłaty są rzadsze niż kapitalizacja, odwrotnie niż w przykładzie 1. Nie będziemy mogli skorzystać z powyższych wzorów, konieczna jest znajomość nowych:
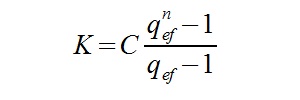
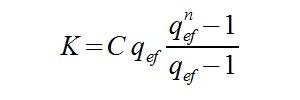
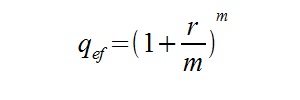
Oznaczenia:
K – łączna kwota wpłat powiększonych o naliczone odsetki
C – przepływ pieniężny
n – ilość okresów wpłat
m – ilość kapitalizacji w jednym okresie wpłaty
r/m – oprocentowanie w danym okresie
Szczególną uwagę należy zwrócić przy obliczaniu q efektywnego. Musimy dobrze policzyć ilość kapitalizacji w jednym okresie wpłaty oraz oprocentowanie w danym okresie. Literka „m” może tu być niestety myląca. Gdybyśmy rozważali 3-letni okres wpłaty i kapitalizację półroczną z oprocentowaniem rocznym 10%, to:
qef = (1 + 0,10/2)^6 = 1,34
Podobnie jak w przypadku pierwszych wzorów, pierwszy z powyższych wzór ma zastosowanie przy płatnościach systematycznych z dołu, tzn. na końcu okresu kapitalizacji (miesiąca/ kwartału/ roku/ …). Drugi natomiast stosuje się przy płatnościach systematycznych z góry – na początku okresu kapitalizacji (inaczej: z wyprzedzeniem).
Rozwiązanie zadania musimy zacząć od wyliczenia q efektywnego:
qef = (1 + 0,06/2)^2 = 1,0609
Następnie korzystamy z drugiego wzoru. Do rozwiązania zadania wystarczy podstawić dane.
K10 = 1 000 * 1,0609 * (1,0609^10 – 1)/(1,0609 – 1)
K10 = 14 042,75
Po 10 latach Klient uzbiera łącznie ponad 14 042,75 zł. Sprawdźmy jednak ile z tej kwoty stanowią uzyskane odsetki?
O = 14 042,75 – 10 * 1 000
O = 14 042,75 – 10 000
O = 4 042,75 zł
Klient zarobi 4 042,75 zł.
0 Komentarze.