Matematyka Finansowa.pl

W jednym z poprzednich wpisów (Wartość przyszła pieniądza – oprocentowanie proste) przedstawiłem metodę obliczenia przyszłej wielkości kapitału przy założeniu braku kapitalizacji odsetek w czasie, np. w trakcie trwania lokaty bankowej. Zakładane oprocentowanie miało być jednak stałe w czasie. W życiu jednak możemy często spotkać się także z oprocentowaniem zmiennym. Poniżej przedstawiam podejście do tej kwestii.

Przykład 1:
Kowalski rok temu założył lokatę bankową o zmiennym oprocentowaniu. Początkowo oferta banku opiewała na 6% w skali rocznej, po 6 miesiącach oprocentowanie zostało jednak obniżone do 5,50%.  Kowalski chciałby wiedzieć jakiego zysku może się spodziewać, ponieważ lokata kończy się na dniach. Kwota jaką zainwestował to 1 500 zł.

Rozwiązanie:
Rozwiązanie tego przypadku nie jest trudne. Należy wykorzystać wzór na przyszłą wartość pieniądza w czasie bez uwzględniania kapitalizacji. Trzeba jednak pamiętać, że oprocentowanie jakie będziemy brali pod uwagę jest średnim rocznym oprocentowaniem lokaty. W tym przykładzie liczymy je następująco:
r = (6/12 * 0,06) + (6/12 * 0,055)
r = 5,75%

Policzmy jeszcze jakich odsetek może spodziewać się Kowalski:
FV = 1 500 zł * (1 + 0,0575)
FV = 1 586,25  zł
Zysk = 1 586,25 zł – 1 500 zł = 86,25 zł
Kowalski na lokacie zarobił 86,25 zł.

Poniżej przedstawiam ogólny wzór na wyliczanie średniego oprocentowania:

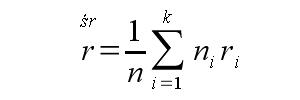
Oznaczenia:
r ^śr – średnie oprocentowanie
n_i – długość podokresu z danym oprocentowaniem (r_i)
r_i – oprocentowanie w podokresie n_i
n – całkowita długość okresu (suma n_i)

Przykład 2:
Bank oferuje półroczną lokatę z oprocentowaniem rosnącym. W pierwszym miesiącu wynosi ono 5% w skali rocznej, natomiast w każdym kolejnym rośnie o 0,50 pkt proc. Ile wynosi średnie oprocentowanie tej lokaty?

Rozwiązanie:
Oczywiście podstawiamy dane do powyższego wzoru.
r^śr = 1/(1/2) * [(1/12 * 0,05) + (1/12 * 0,055) + (1/12 * 0,06) + (1/12 * 0,065) + (1/12 * 0,07) + (1/12 * 0,075)]
r^śr = 6,25%