Matematyka Finansowa.pl

Kontynuujemy dalej tematykę płatności systematycznych, którą poruszyłem w poprzednich wpisach:
– Płatności systematyczne – oprocentowanie złożone (cz. 1)
– Płatności systematyczne – oprocentowanie złożone (cz. 2))
Ciągle mamy do czynienia z oprocentowaniem złożonym. Dotychczas jednak rozważaliśmy przykłady z rocznym okresem kapitalizacji i wpłat systematycznych. Tym razem sprawdzimy jak kształtuje się przyszła wartość sumy wpłat dla kapitalizacji śródrocznej. Ciągle jednak zakładamy, że okresy kapitalizacji i kolejnych wpłat są równe.

Aby dokładniej zrozumieć korzyści dla Klienta wynikające z zastosowania częstszych kapitalizacji wykorzystamy zadania z poprzednich wpisów (konieczna będzie jednak drobna ich modyfikacja).

Przykład 1:
Klient zamierza przez 10 lat wpłacać po 250 zł rocznie na konto oszczędnościowe. Wpłaty będą dokonywane na początku każdego kwartału, natomiast bank oferuje oprocentowanie na poziomie 6% rocznie (kapitalizacja kwartalna). Ile odsetek (łącznie) klient otrzyma po 3, 7 i 10 latach oszczędzania?

Jest to przykład z wpisu „Płatności systematyczne – oprocentowanie złożone (cz. 2)”. Różnica polega na tym, że poprzednio Klient wpłacał 1 000 zł rocznie, teraz zaś 250 zł kwartalnie (sumując, rocznie będzie to także 1 000 zł). Ponadto kapitalizacja roczna została zastąpiona kwartalną.

Aby rozwiązać tego typu przykład musimy zmodyfikować wzór z przytoczonego powyżej wpisu. Modyfikacja dotyczy jedynie zastąpienia oprocentowania „r” oprocentowaniem „r/m”, oraz dodania zmiennej „m” – ilości kapitalizacji w jednym okresie (roku).

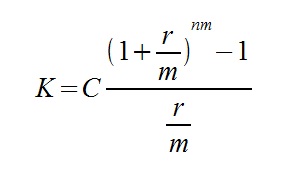
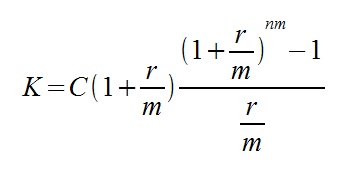
Oznaczenia:
K – łączna kwota wpłat powiększonych o naliczone odsetki
C – przepływ pieniężny
n – ilość okresów (lat)
m – ilość kapitalizacji w jednym okresie (np. roku)
r – oprocentowanie w danym okresie (roku)

Pierwszy wzór stosuje się przy płatnościach systematycznych z dołu, tzn. na końcu okresu kapitalizacji (miesiąca/ kwartału/ roku/ …). Drugi natomiast dotyczy płatności systematycznych z góry – na początku okresu kapitalizacji (inaczej: z wyprzedzeniem).

W zadaniu mamy do czynienia z płatnościami systematycznymi z góry. Stosujemy zatem drugi z wzór.

K3 = 250 * (1 + 0,06/4) * ((1 + 0,06/4)^(3*4) – 1)/(0,06/4)
K3 = 250 * 13,24
K3 = 3 309,21 zł

K7 = 250 * (1 + 0,06/4) * ((1 + 0,06/4)^(7*4) – 1)/(0,06/4)
K7 = 250 * 35
K7 = 8 749,68 zł

K10 = 250 * (1 + 0,06/) * ((1 + 0,06/4)^(10*4) – 1)/(0,06/4)
K10 = 250 * 55,08
K10 = 13 770,48 zł

Przypomnijmy jakie oszczędności zgromadził Klient po 3, 7 i 10 latach przy wpłatach 1 000 zł raz w roku:
K3 = 3 309,21 zł
K7 = 8 749,68 zł
K10 = 13 770,48 zł

Okazuje się zatem, że zdecydowanie bardziej opłaca się wpłacać mniejsze kwoty, ale za to częściej. Oczywiście bank powinien oferować również częstszą niż raz w roku kapitalizację odsetek.

Przykład 2:
Kowalski zamierza oszczędzać na emeryturę. Policzył, że będzie mógł kwartalnie odłożyć po 200 zł. Wpłaty będzie dokonywał na specjalnie utworzony program systematycznego oszczędzania. Jaką kwotę uzbiera po 30 latach przy założeniu nominalnej 6%, 7% oraz 8% stopy zwrotu oraz kapitalizacji kwartalnej odsetek.

Także w tym zadaniu także mamy do czynienia z płatnościami systematycznymi z góry. Stosujemy zatem drugi z wzór.

Wyliczenie dla 6% rocznej stopy zwrotu:
K = 200 * (1 + 0,06/4) * ((1 + 0,06/4)^(30*4) – 1)/(0,06/4)
K = 200 * 336,26
K = 67 251,50 zł

Wyliczenie dla 7% rocznej stopy zwrotu:
K = 200 * (1 + 0,07/4) * ((1 + 0,07/4)^(30*4) – 1)/(0,07/4)
K = 200 * 408,12
K = 81 623,08 zł

Wyliczenie dla 8% rocznej stopy zwrotu:
K = 200 * (1 + 0,08/4) * ((1 + 0,08/4)^(30*4) – 1)/(0,08/4)
K = 200 * 498,02
K = 99 604,66 zł

Widzimy zatem, że im większa oczekiwana stopa zwrotu, tym większe zyski po x-latach oszczędzania. Warto jednak dodać, że ryzyko związane z inwestycją jest także większe. Oczywiście także w tym przykładzie (szczególnie przy 8% stopie zwrotu), zauważyć możemy pozytywny wpływ zwiększenia częstotliwości kapitalizacji odsetek na uzyskany efekt końcowy.