W życiu najczęściej spotykamy się z pojęciem wartości przyszłej pieniądza. Warto jednak wiedzieć jak ustalić dzisiejszą (bieżącą) wartość pieniądza. Matematyka finansowa tego typu operacje określa mianem dyskontowania. Jest to operacja odwrotna w stosunku do oprocentowania. W tym wpisie przyjrzymy się dyskontowaniu prostemu, czyli takiemu, w przypadku którego nie mamy do czynienia z pojęciem kapitalizacji.
Operacje dyskontowania pomogą nam zrozumieć poniższe przykłady. Rozwiązywać je będziemy przy wykorzystaniu poniższego wzoru. Jest to przekształcony wzór na przyszłą wartość pieniądza – dokładnie opisany we wpisie Wartość przyszła pieniądza – oprocentowanie proste.
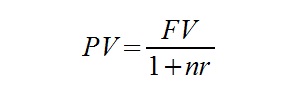
Oznaczenia:
FV – wartość przyszła (Future Value)
PV – wartość bieżąca (Present Value)
n – ilość okresów
r – oprocentowanie
Przykład 1:
Sąsiad jest winny Kowalskiemu 950 zł. Obiecał mu oddać środki jutro, niemniej zaproponował, że jeśli Kowalski przedłuży termin zwrotu o rok, to odda mu 1 000 zł. Czy Kowalski powinien się zgodzić na propozycję? Oprocentowanie lokaty rocznej w jego banku wynosi 5%.
Wartość bieżąca pożyczki to 950 zł. Przyjmijmy, że jest to wartość dla wariantu pierwszego. Wariantem drugim będzie propozycja sąsiada – z tym, że tu mamy daną jedynie wartość przyszłą. Wykorzystajmy zatem powyższy wzór by obliczyć wartość bieżącą. Mamy wszystkie niezbędne dane.
PV = 1 000 / (1 + 0,05*1)
PV = 1 000 / 1,05
PV = 952,38 zł
Wartość bieżąca dla drugiego wariantu jest wyższa niż dla pierwszego. Wynika z tego, że Kowalski powinien przystać na propozycję, ponieważ jest ona korzystna. Sprawdźmy to jeszcze obliczając wartość przyszłą 950 zł (wariant pierwszy).
FV = 950 * (1 + 0,05)
FV = 950 * 1,05
FV = 997,50 zł
Przykład 2:
Za 5 miesięcy Kowalski ma otrzymać z banku 15 000 zł. Jaka jest wartość bieżąca oszczędności, jeśli oprocentowanie lokat w banku wynosi 8% (w skali roku)?
PV = 15 000 / (1 + 0,08 * 5 / 12)
PV = 15 000 / 1,03
PV = 14 516,13 zł
Bieżąca wartość oszczędności Kowalskiego wynosi 14 516,13 zł.
2 Komentarze.