Matematyka Finansowa.pl

Załóżmy, że firma kupuje nową maszynę produkcyjną. Ma za nią zapłacić dopiero za rok. Producent może jednak przyjąć zapłatę wcześniej. Firma płacąc dziś otrzyma 5% rabatu. Rabat ten nazywamy dyskontem handlowym. Zależy ono od kwoty oddawanej i w gruncie rzeczy trzeba je zapłacić z góry. Odwrotnie jest w przypadku dyskonta prostego (Wartość bieżąca pieniądza – dyskontowanie proste). Kiedyś dyskonto handlowe było bardzo popularne w rozliczeniach między firmami, dziś straciło mocno na znaczeniu. Obecnie stosujemy je głównie w rachunku weksli i bonów skarbowych. Przeanalizujmy kilka zadań.

Przykład 1:
Firma A zastanawia się nad kupnem nowej ciężarówki. Jej cena u dealera to 450 000 zł przy płatności za rok lub 430 000 przy płatności teraz. Oblicz wielkość dyskonta handlowego oraz stopę dyskontową.

Do rozwiązania zadania konieczna będzie znajomość poniższego wzoru:

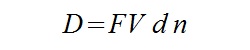
Oznaczenia:
FV – wartość przyszła (Future Value)
n – ilość okresów (lat)
d – stopa dyskontowa

Stopa dyskontowa jest stosunkiem dyskonta handlowego do kwoty należnej wierzycielowi.

Rozwiążmy zatem powyższe zadanie. Zacznijmy od obliczenia wielkości dyskonta. Niestety nie mamy (jeszcze) podanej stopy dyskontowej, stąd nie skorzystamy z powyższego wzoru. Mamy zaś wartość bieżącą i przyszłą. Dyskonto handlowe będzie różnicą pomiędzy obiema wartościami.

D = FV – PV
D = 450 000 – 430 000
D = 20 000

Mając wielkość dyskonta możemy obliczyć stopę dyskontową.

d = D / FV
d = 20 000 / 450 000
d = 0,0444
d = 4,44%

Sprawdźmy jeszcze poprawność powyższych obliczeń podstawiając uzyskane wyniki do powyższego wzoru.

D =? FV * d * n
20 000 =? 450 000 * 0,0444 * 1
20 000 =? 19 980

Możemy przyjąć, że obie wartości są sobie równe. Różnica wynika z zaokrąglenia stopy dyskontowej.

Przykład 2:
Firma XYZ sprzedaje nowe maszyny do produkcji okolicznościowych monet. Ich koszt to 20 000 zł. Firma na zapłatę daje 3 miesiące. Oferuje jednak rabaty za wcześniejsze uregulowanie należności. Za każdy miesiąc 2%, czyli łącznie 6% dyskonta handlowego przy płatności w chwili odbioru maszyny. Oblicz cenę maszyny przy płatności:
– w chwili zakupu,
– po miesiącu od zakupu,
– po dwóch miesiącach od zakupu,

Zadanie nie jest trudne, podstawiamy odpowiednie dane do wzoru z początku wpisu.

D₀ = 20 000 * 0,02 * 3
D₀ = 20 000 * 0,06
D₀ = 1 200

Cena maszyny przy płatności w chwili zakupu wynosi 18 800 zł (20 000 – 1 200).

D₁ = 20 000 * 0,02 * 2
D₁ = 20 000 * 0,04
D₁ = 800

Cena maszyny przy płatności po miesiącu od zakupu wynosi 19 200 zł (20 000 – 800).

D₂ = 20 000 * 0,02 * 1
D₂ = 20 000 * 0,02
D₂ = 400

Cena maszyny przy płatności po dwóch miesiącach od zakupu wynosi 19 600 zł (20 000 – 400).

Oczywiście cena maszyny przy płatności po trzech miesiącach od jej zakupu wynosi 20 000, jest to dana z zadania.