Matematyka Finansowa.pl

Wewnętrzna stopa zwrotu (IRR – Internal Rate of Return) jest, podobnie jak księgowa stopa zwrotu, jedną z metod oceny efektywności ekonomicznej projektów inwestycyjnych. Jest to jednak zdecydowanie bardziej złożona metoda. Przede wszystkim uwzględnia ona zmiany wartości pieniądza w czasie. Pozwala to na określenie rzeczywistej stopy dochodu z projektu inwestycyjnego. Generowany dochód może zaś być różny w czasie. W poszczególnych okresach (standardowo są to lata) jest on dyskontowany a następnie sumowany i porównywany z wartością inwestycji. IRR jest taką stopą dyskontową dla której wartość zdyskontowanych przepływów jest równa wartości inwestycji. Nie trudno zatem zauważyć, że im wyższa wewnętrzna stopa zwrotu, tym inwestycja może być potencjalnie bardziej opłacalna.

IRR ma wiele zalet. Jest przede wszystkim stosunkowo prosta do obliczenia i bardzo prosta w interpretacji. Ponadto zakłada dyskontowanie wszystkich przepływów pieniężnych, obejmujących cały cykl inwestycyjny, dzięki czemu doskonale określa jego efektywność. Za wadę wewnętrznej stopy zwrotu uznać należy brak uniwersalności. Nie nadaje się do oceny efektywności ekonomicznej projektów złożonych i nietypowych.

Zapoznajmy się najpierw z poniższym wzorem:

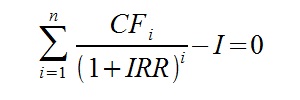
Oznaczenia:
I – wartość inwestycji
CF_i – przepływ pieniężny w i-tym okresie
n – długość procesu inwestycyjnego

Przykład 1:
Przedsiębiorca zamierza kupić samochód dostawczy. Jego koszt to 85 000 zł. Szacuje się, że przez pierwsze cztery lata inwestycja przyniesie po ok. 25 000 zł dochodu. W kolejnych dwóch latach po ok. 20 000 zł. W siódmym roku będzie to ok. 10 000 zł. Następnie najwłaściwszym rozwiązaniem będzie sprzedaż samochodu za ok. 15 000 zł (naprawy będą zbyt czaso i kosztochłonne). Jaka jest wewnętrzna stopa zwrotu inwestycji?

Stwórzmy sobie następującą tabelkę:
0: -85 000
1: 25 000
2: 25 000
3: 25 000
4: 25 000
5: 20 000
6: 20 000
7: 10 000
8: 15 000

Powyższa tabelka pokazuje nominalne przepływy pieniężne w poszczególnych latach cyklu inwestycyjnego. Poszukujemy IRR. Niestety ręcznie będzie je bardzo trudno znaleźć (patrz wzór). Jedyną prostą ręczną metodą jest zgadywanie wewnętrznej stopy zwrotu i podstawianie jej do wzoru. Gdy suma zdyskontowanych przepływów będzie większa od zera, zmniejszamy jej wartość, gdy będzie mniejsza od zera – przyjęte IRR jest zbyt niskie. Innym rozwiązaniem jest skorzystanie z Excela (alternatywnie Calc z pakietu Open Office). Dla powyższego zadania IRR wynosi 20,32%. Poniżej znajdują się zdyskontowane wartości przepływów w kolejnych latach.

0: -85 000
1: 20 778
2: 17 268
3: 14 352
4: 11 928
5: 7 930
6: 6 591
7: 2 739
8: 3 414

Przykład 2:
Przedsiębiorca rozważa zakup nowych zestawów komputerowych. Z jednej strony ich zakup pozwoli wygenerować większe zyski – komputery będą szybsze a dzięki nowemu oprogramowaniu będzie można przyjąć atrakcyjne zlecenia. Z drugiej jednak strony przedsiębiorca będzie musiał zaciągnąć kredyt bankowy, którego oprocentowanie nie jest korzystne. Rzeczywiste oprocentowanie pożyczki wynosi bowiem 14,50%. Właściciel rozważa zatem dwie możliwości. Pierwsza to zakup 3 prostych zestawów za 24 000 zł. Inwestycja ta pozwoli wygenerować w kolejnych 4 latach po 8 000 zł dodatkowego zysku. Drugą opcją jest zakup nowoczesnego sprzętu za 56 000 zł. Koszt spory, ale i zyski wysokie – właściciel zakłada, że będzie to ok. 19 000 zł rocznie przez najbliższe 4 lata. Co powinien zrobić przedsiębiorca?

Aby rozwiązać to zadanie powinniśmy obliczyć IRR dla obu wariantów inwestycji. I tym razem polecam skorzystanie z Excela lub Calca.

IRR₁ = 12,59%
IRR₂ = 13,44%

Korzystniejsza jest druga propozycja. Czy jednak na pewno właściciel firmy powinien decydować się na inwestycję? Nie. Rzeczywiste oprocentowanie kredytu bankowego jest bowiem wyższe od wewnętrznej stopy zwrotu. Właściciel firmy zatem nie tylko nie zarobi na inwestycji, ale nawet straci. Powinien zatem pomyśleć nad innym rozwiązaniem.