W poprzednim wpisie przedstawiłem tematykę dyskontowania składanego rent. Oczywiście nie całą. Obiecałem poszerzyć wiedzę w kolejnym wpisie. Obietnica zatem zostanie dotrzymana. O ile poprzednim razem przyjęliśmy założenie, że kapitalizacja odsetek występuje jedynie raz w roku, tak teraz zajmiemy się kapitalizacją śródroczną (np. kwartalną czy też miesięczną). Według mnie jest to najwłaściwsze podejście do rozwiązywania zadań związanych z dyskontowaniem strumieni płatności. Banki bowiem w zdecydowanej większości stosują kapitalizację miesięczną. Ostatnio „modna” stała się kapitalizacja dzienna (czyli powoli zbliżamy się do kapitalizacji ciągłej), niemniej spowodowane jest to jedynie lukami w prawie, które mają być wkrótce zlikwidowane. Na pewno zaś stosowanie częstej kapitalizacji nie jest korzystne dla sektora bankowego.
Przykład 1:
Doradca w banku zaproponował Kowalskiemu systematyczne oszczędzanie na rachunku oszczędnościowym. Nowy produkt banku zakłada, że jeśli Klient zobowiąże się do regularnych wpłat przez kolejne 20 lat, to będzie miał zagwarantowany roczny zysk na poziomie 3% (bez względu na sytuację makroekonomiczną w kraju i wysokość stóp procentowych). Co ważne, kapitalizacja na rachunku będzie kwartalna. Kowalski musi jedynie zobowiązać się, że kwartalnie wpłaci 100 zł. Jaką kwotę Kowalski otrzyma po 20 latach oszczędzania oraz jaka jest bieżąca wartość 80 przyszłych wpłat (20 lat po 4 wpłaty rocznie)? Wpłaty będą dokonywane na początku każdego kwartału.
Poniżej przedstawiam wzory, które pomogą nam dyskontować renty składane przy założeniu kapitalizacji śródrocznej.
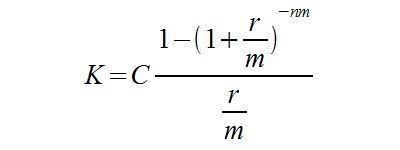
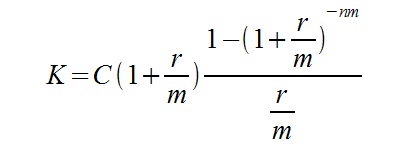
K – łączna kwota zdyskontowanych płatności
C – przepływ pieniężny
n – ilość okresów (lat)
m – ilość kapitalizacji w jednym okresie (np. roku)
r – oprocentowanie nominalne w danym okresie (np. roku)
Pierwszy wzór stosuje się przy płatnościach systematycznych z dołu, tzn. na końcu roku. Drugi natomiast dotyczy płatności systematycznych z góry – na początku roku (inaczej: z wyprzedzeniem).
Wróćmy zatem do zadania. Mamy do obliczenia dwie rzeczy: kwotę Kowalski zaoszczędzi po 20 latach oraz bieżącą wartość 80 przyszłych wpłat. Pierwszą z tych wartości obliczymy wykorzystując wzór prezentowany już jakiś czas temu we wpisie Płatności systematyczne – oprocentowanie złożone (cz. 3). Podstawmy zatem posiadane dane do wzoru.
K = 100 (1 + 0,03/4) * (((1 + 0,03/4)^(20*4) – 1) / (0,03/4))
K = 100,75 * (0,82/00,75)
K = 100,75 * 109,07
K = 10 989,06 zł
Kowalski zatem z banku otrzyma po 20 latach oszczędzania niespełna 11 000 zł. Nie jest to dużo biorąc pod uwagę fakt, że przez te 20 lat wpłaci do banku 8 000 zł. Sprawdźmy jednak jaka jest bieżąca wartość tych 80 wpłat po 100 zł.
K = 100 * (1 + 0,03/4) * ((1 – (1 + 0,03/4)^(-20*4)) / (0,03/4))
K = 100,75 * (0,45/0,0075)
K = 6 044,44 zł
Wartość bieżąca wpłat na konto oszczędnościowe to 6 044,44 zł. Zakładany zysk w perspektywie 20 lat to 4 944,62 zł. Nie jest to dużo. Kwota zysku byłaby zdecydowanie wyższa, gdyby bank zaproponował korzystniejsze oprocentowanie.
Przykład 2:
Kowalski skorzystał z propozycji swojego Doradcy. Zobowiązał się wpłacać na koniec każdego roku 1 000 zł na specjalny produkt inwestycyjny opakowany w polisę na życie. Rocznie zarobi na tym 2%, ale za to jest ubezpieczony.
Policz jaka jest wartość wpłacanych środków po 10 latach.
Rozwiązanie tego zadania jest bardzo proste. Po prostu podstawiamy dane do pierwszego wzoru z niniejszego wpisu.
K = 1 000 * ((1 – (1 + 0,02/1)^(-10*1)) / (0,02/1))
K = 1 000 * (0,18/0,02)
K = 1 000 * 8,98 zł
K = 8 982,59 zł
Wartość bieżąca 10 przyszłych wpłat po 1 000 zł każda wynosi niespełna 9 000 zł.
0 Komentarze.