We wpisie Dyskontowanie rent prostych poruszyłem tematykę dyskontowania ciągów płatności (rent). Wszystko byłoby w porządku, gdyby nie pewien fakt – w rzeczywistości bardzo rzadko mamy do czynienia z dyskontowaniem prostym strumieni płatności. Znacznie częściej spotykamy się z zadaniami wymagającymi zastosowania procentu składanego. Dotyczy to w szczególności zadań z wieloletnim okresem inwestycji/ pożyczki… Warto zatem przypomnieć sobie poprzedni wpis a następnie poszerzyć wiedzę o niniejsze opracowanie (i kolejne, opublikuję je za kilka dni, tematyka jest bowiem mocno rozbudowana).
Przykład 1:
Doradca w Banku X przedstawił Kowalskiemu następującą propozycję – jeśli zdecyduje się Pan odkładać raz w roku 500 zł na specjalnie otwarte konto oszczędnościowe przez okres 30 lat, my zagwarantujemy Panu roczne oprocentowanie w wysokości 5% w każdym roku oszczędzania. Kowalski chciałby wiedzieć ile po 30 latach zgromadzi środków, oraz jaka jest wartość bieżąca przyszłych wpłat na konto. Niestety Doradca w Banku X nie potrafił udzielić odpowiedzi na te pytania.
Sprawdźmy jaką kwotę zgromadziłby Kowalski po 30 latach, gdyby skorzystał z propozycji swojego Doradcy. Odpowiedni wzór został przedstawiony we wpisie Płatności systematyczne – oprocentowanie złożone (cz. 2).
K = 500 * (1 + 0,05) * (((1 + 0,05)^30 – 1)/((1 + 0,05) – 1))
K = 500 * 1,05 * (3,32 / 0,05)
K = 500 * 1,05 * 66,44
K = 34 880,39 zł
Kowalski zatem na koncie oszczędnościowym po 30 latach oszczędzania będzie miał niespełna 35 000 zł.
Sprawdźmy teraz jaka jest wartość bieżąca 30 rocznych wpłat po 500 zł. Skorzystać będziemy musieli jednak z zupełnie nowego wzoru. Przedstawiam go poniżej.
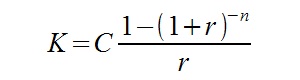
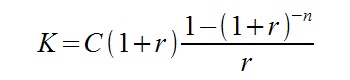
q = 1 + r
q ≠ 1
Oznaczenia:
K – łączna kwota zdyskontowanych płatności
C – przepływ pieniężny
n – łączna ilość wpłat
r – oprocentowanie
Pierwszy wzór stosuje się przy płatnościach systematycznych z dołu, tzn. na końcu roku. Drugi natomiast dotyczy płatności systematycznych z góry – na początku roku (inaczej: z wyprzedzeniem).
By rozwiązać powyższe zadanie podstawiamy posiadane dane do wzoru drugiego.
K = 500 * (1 + 0,05) * ((1 – (1 + 0,05)^(-30)) / 0,05)
K = 500 * 1,05 * 15,37
K = 8 070,54 zł
Wartość bieżąca przyszłych 30 wpłat Kowalskiego na konto oszczędnościowe wynosi 8 070,54 zł.
Przykład 2:
Doradca inwestycyjny zaproponował Kowalskiemu inwestycję w fundusze inwestycyjne. Jeśli zobowiąże się do systematycznych wpłat przez 15 lat w kwocie 250 zł rocznie, to będzie miał zagwarantowany roczny zysk na poziomie 4%. Jaką minimalną kwotę Kowalski otrzyma po 15 latach oszczędzania oraz jaka jest bieżąca wartość 15 przyszłych wpłat (zakupów jednostek uczestnictwa funduszy inwestycyjnych)?
Minimalną kwotę jaką Kowalski otrzyma po 15latach inwestycji obliczymy za pomocą wzoru z wpisu Płatności systematyczne – oprocentowanie złożone (cz. 2).
K = 250 * (1 + 0,04) * (((1 + 0,04)^15 – 1)/((1 + 0,04) – 1))
K = 250 * 1,04 * (1,80 / 0,04)
K = 250 * 1,04 * 20,02
K = 5 256,19 zł
Skoro wiemy już na jaką kwotę Kowalski może liczyć po 15 latach inwestowania, sprawdźmy jaka jest bieżąca wartość koniecznych wpłat. Korzystamy z wzoru przedstawionego z tym wpisie (wpłaty z góry).
K = 250 * (1 + 0,04) * ((1 – (1 + 0,04)^(-15)) / 0,04)
K = 250 * 1,04 * 11,12
K = 2 890,78 zł
Bieżąca wartość inwestycji Kowalskiego to 2 890,78 zł. Z inwestycji tej może oczekiwać minimalnego zysku na poziomie 2 365,41 zł (5 256,19 – 2 890,78).
0 Komentarze.