Z poprzedniego wpisu (Jak wyliczyć ratę równą kredytu?) wiecie jak wyliczyć ratę równą kredytu. Czas na ratę malejącą, korzystniejszą dla Klienta (o ile głównym wyznacznikiem jest całkowity koszt kredytu).
Zacznijmy od wzoru, przeanalizujemy go następnie w zadaniach.
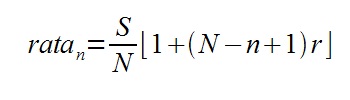
Oznaczenia:
S – kwota zaciągniętego kredytu (kwota brutto, wraz z kosztami okołokredytowymi)
N – ilość rat
n – numer poszukiwanej raty
r – oprocentowanie nominalne dla okresu
Przykład 1:
Kowalski zaciągnął szybki kredyt gotówkowy z swoim banku. Kwota jaką otrzymał to 4 000 zł, okres kredytowania to 24 miesiące. Wyliczyć wysokość pierwszych trzech rat malejących przy oprocentowaniu w wysokości 15% oraz 17%.
Korzystamy z powyższego wzoru. Oprocentowanie musimy podzielić przez 12, tyle rat mamy bowiem w roku.
rata1 = 4 000/24 [1 + (24 – 1 + 1) * 0,15/12]
rata1 = 166,67 * 1,3
rata1 = 216,67 zł
rata2 = 4 000/24 [1 + (24 – 2 + 1) * 0,15/12]
rata2 = 166,67 * 1,2875
rata2 = 214,59 zł
rata3 = 4 000/24 [1 + (24 – 3 + 1) * 0,15/12]
rata3 = 166,67 * 1,275
rata3 = 212,50 zł
rata1 = 4 000/24 [1 + (24 – 1 + 1) * 0,17/12]
rata1 = 166,67 * 1,34
rata1 = 223,34 zł
rata2 = 4 000/24 [1 + (24 – 2 + 1) * 0,17/12]
rata2 = 166,67 * 1,326
rata2 = 220,98 zł
rata3 = 4 000/24 [1 + (24 – 3 + 1) * 0,17/12]
rata3 = 166,67 * 1,312
rata3 = 218,62 zł
Analizując powyższy przykład łatwo dojść do wniosku, że oprocentowanie kredytu odgrywa bardzo dużą rolę. Mimo niewielkiej różnicy na poziomie 2 pkt proc., rata dla Klienta jest droższa o ok. 6-8 zł. W całym okresie kredytowania daje to sporą różnicę w kosztach.
Przykład 2:
Kowalski otrzymał ofertę kredytu gotówkowego w swoim banku. Bank, dla kwoty 10 000 zł, proponuje oprocentowanie w wysokości 16,90% oraz brak prowizji za przyznanie kredytu. Kowalski może spłacać raty kwartalnie, okres kredytowania to 3 lata. Wyliczyć wysokość pierwszych czterech rat malejących.
Korzystamy z tego samego wzoru co w przykładzie 1.
rata1 = 10 000/12 [1 + (12 – 1 + 1) * 0,169/4]
rata1 = 833,33 * 1,507
rata1 = 1 255,83 zł
rata2 = 10 000/12 [1 + (12 – 2 + 1) * 0,169/4]
rata2 = 833,33 * 1,4648
rata2 = 1 220,62 zł
rata3 = 10 000/12 [1 + (12 – 3 + 1) * 0,169/4]
rata3 = 833,33 * 1,4225
rata3 = 1 185,42 zł
rata4 = 10 000/12 [1 + (12 – 4 + 1) * 0,169/4]
rata4 = 833,33 * 1,3803
rata4 = 1 150,21 zł
Czy w we wzorze nie powinno być ?
rata = S / N * (1 + (N – n + 1) * r / m)
brakuje /m
Wzór jest prawidłowy, jest to jego ogólna postać. „r” to oprocentowanie nominalne dla okresu (czyli dla miesiąca/kwartału/roku). Jeśli zaś w zadaniu r będzie oprocentowaniem rocznym a raty płacone będą miesięcznie to r dzielimy przez 12, zgodnie z wzorem przytoczonym w komentarzu.